Frequentemente a gente vê algumas aplicações e projetos que usam algoritmos de FFT para gerar a DFT, por exemplo analisadores de espectro, detetores de frequência, afinadores, medidores de distorção, etc.
Mas o que vem a ser a tal da DFT e FFT e como elas funcionam ?
DFT quer dizer transformada discreta de Fourier, que faz parte da família das transformadas de Fourier, cuja aplicação na eletrônica e processamento de sinais é uma forma de pegar um sinal no domínio do tempo e representá-lo no domínio da frequência, informando a sua amplitude e fase. A FFT (transformada rápida de Fourier) é apenas um algoritmo usado em computadores para gerar a DFT. A DFT é chamada de discreta porque lida com um sinal discreto, isto é, de pontos da onda amostrados por períodos de tempo iguais, digitalizados e armazenados numa matriz de dados. Esses dados serão processados digitalmente e a partir deles obtemos dados de amplitude e fase dos componentes da forma de onda.
Existe muita literatura sobre o assunto, mas é muito difícil se encontrar explicações que não usem fórmulas complexas e de difícil compreensão. Eu só encontrei dois artigos que explicam com gráficos e passo a passo uma forma de se fazer a DFT de um sinal, um deles chamado de "Fourier Transform for Dummies" e o outro na revista Nuts and Volts chamado de "DFT basics". Ambos mostram gráficos (que eu reproduzo aqui) e usam planilhas eletrônicas para calcular a DFT, mas nada tão complicado que não possa ser feito com papel e lápis e calculadora. Obviamente podemos usar programas de computador ou um microcontrolador (melhor um DSP - digital signal processor) pra amostrar o sinal e realizar esses cálculos.
A seguir a tradução que fiz do primeiro artigo citado:
=============================
Transformada de Fourier para iniciantes
O que é uma transformada de Fourier ?
A transformada (discreta) de Fourier é um método de detecção de quais frequências estão presentes em uma amostra de forma de onda. Dado um conjunto de dados amostrados e uma frequência, a transformada vai lhe dar a amplitude e a fase daquela frequência dentro dos dados amostrados.
Por exemplo, digamos que você queira saber se uma componente de 1kHz está presente em seus dados amostrados. A transformada de Fourier vai lhe dizer a amplitude e a fase de qualquer componente de 1kHz nos seus dados amostrados.
Como funciona ?
Vamos estudar um simples exemplo ideal. Digamos que uma forma de onda senoidal de 5V e 1kHz seja amostrada a 30000 amostras por segundo durante 1 milisegundo. Se obteria 30 pontos de dados (samples), representando exatamente uma onda completa. Nesse momento vamos assumir que a amostragem tenha começado no 0 grau (azul no gráfico).
Agora se quisermos detetar 1kHz, temos que multiplicar o valor de cada ponto amostrado por um sinal senoidal de 1V a 1kHz (magenta no gráfico). As duas ondas tem o mesmo formato e mesma fase, assim quando ambas são positivas, obtemos um produto positivo (resultado da multiplicação) representado pela linha amarela no gráfico. Da mesma forma, quando ambos sinais forem negativos, também obteremos um produto positivo (menos vezes menos = mais). Agora se pegarmos a soma dos 30 produtos obteremos o valor de 75. Precisamos então dividir essa soma por 15 e obter o valor 5. Isso nos informa que a amostra contém uma componente senoidal de 1kHz e 5V de amplitude.
Nota: esse método é o de correlação de sinais. Ao fazermos a multiplicação do sinal amostrado por um sinal que queremos detetar (chamado de sinal base), descobrimos se há correlação (similaridade) entre os dois sinais. Quanto maior o casamento entre os dois sinais, maior será a correlação e portanto maior o valor encontrado.
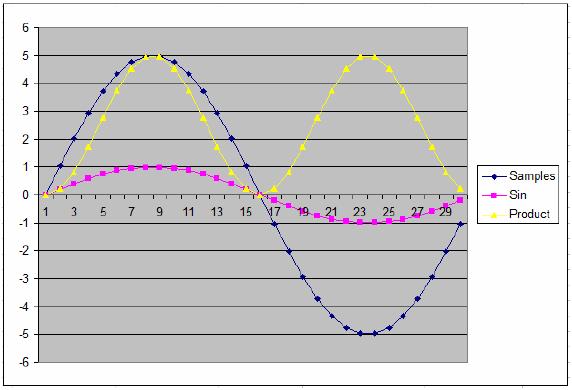
Vamos fazer o mesmo processo, mas tentando detetar um componente de 2kHz na amostra.
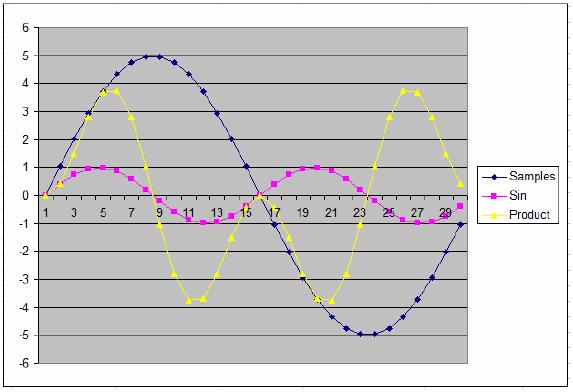
Agora podemos ver que os produtos (amarelo no gráfico) ficam positivos e negativos. E se somarmos todos os valores dos pontos dos produtos, vamos obter zero. Isso indica que
não há uma componente de 2kHz nos dados amostrados.
Nota: ou seja não há correlação entre o sinal amostrado e o sinal base, por isso o valor obtido é zero ou muito baixo.
O que acontece se os dados amostrados não começarem no zero grau ?
Vamos supor que os dados comecem aos 45 graus ao invés de 0 grau.
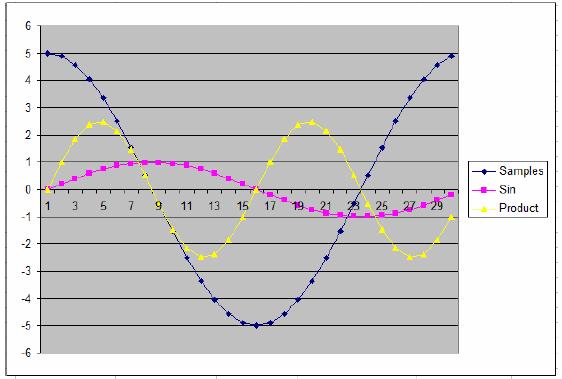
Como podemos ver, a forma de onda dos produtos fica tanto positiva como negativa. De fato, se somarmos os produtos, vamos obter zero. Hmmmm, isso é um problema.
Se resolve esse problema fazendo o mesmo processo de multiplicação duas vezes, uma vez com uma onda senoidal e de novo com uma onda cosenoidal. O produto da onda cosenoidal será similar a do nosso produto original, exceto que ela estará defasada.
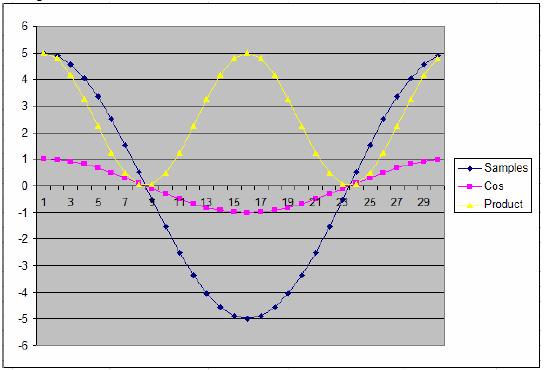
Ok, e se tivermos uma amostra com uma defasagem mais atípica, por exemplo 20 graus ?
Nesse caso é que usamos a soma dos produtos da onda senoidal e da onda cosenoidal e fazemos a composição dos dois valores como X e Y onde o valor da amplitude será A = raiz (X^2 + Y^2) e a fase será o arcotangente de Y/X.
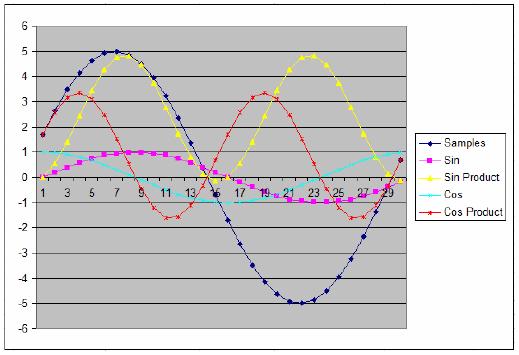
Nos dados mostrados acima, a soma dos produtos da onda senoidal é 4,69846 (depois de dividido por 15) e a soma dos produtos da onda cosenoidal é 1,71010 (depois de dividido por 15). Para encontrar a amplitude usamos: raiz (4,69846^2 + 1,71010^2) = 5 e arcotangente (1,71010/4,69846) = 20°
Isso quer dizer que nossa amostra contém um componente senoidal de 1kHz com amplitude de 5 e uma fase de 20 graus.

