Conforme comentei em outro tópico, coloco aqui o texto sobre valor eficaz, que espero clarificar mais um conceito muito usado por todos.
Pequena aula sobre valor eficaz ou rms
Um sinal (tensão ou corrente) de natureza alternada e periódica possui algumas características que ajudam a entender a sua forma e propriedades. Assim um sinal alternado puro seria a onda senoidal, que apresenta somente um componente espectral (harmônico), diferentemente de uma onda quadrada ou triangular que possui infinitos componentes harmônicos. Um sinal alternado também tem um período (tempo ou comprimento de um ciclo) em que ele torna a se repetir no formato. Relacionado ao período, o sinal tem a sua frequência (que é o inverso do período). Se um sinal estiver deslocado de outro de mesma frequência, dizemos que há um defasamento entre eles, e o valor desse deslocamento é chamado de fase (um ângulo). Outra característica do sinal alternado é a sua amplitude, ou seja a diferença entre o ponto máximo de seu valor e o ponto mínimo.
Mas nenhum desses atributos descreve bem ou traduz o seu valor em termos de utilização de tensão ou corrente. Por exemplo, ao usarmos uma bateria de carro, sabemos que a tensão nominal dela é de 12Vdc, e podemos ligar aparelhos e circuitos que usem ou aceitem 12Vdc como tensão de alimentação.
Já no caso de um gerador de tensão alternada, qual seria esse valor que serviria como referência para utilização com máquinas e aparelhos ? O sinal alternado é pulsante e continuamente variável no seu valor a uma determinada frequência, muitas vezes tendo valores máximos (de pico) positivos e valores mínimos negativos. Seria válido usar o valor de pico ? (mesmo sabendo que durante muito pouco tempo do ciclo ele fica nesse valor). Seria válido usar um valor médio ? (sabendo que havendo excursão simétrica do sinal do lado positivo como do lado negativo, teria uma média igual a zero). Pensou-se então em descobrir um valor para o sinal alternado que fizesse o mesmo trabalho que uma tensão ou corrente contínua de valor numérico equivalente. Sabendo-se que aplicando uma tensão contínua a uma resistência faz circular uma corrente que vai por efeito joule gerar calor (dissipar potência = realizar trabalho em termos físicos) na resistência e que podemos aplicar uma tensão alternada de valor x que vai dissipar a mesma potência (a corrente apesar de ficar num vai e vem, também realiza o aquecimento da resistência, não dependendo da direção).
Convencionou-se chamar de valor eficaz a esse valor de tensão (ou corrente) alternada equivalente a um valor de tensão (ou corrente) contínua que produzisse a mesma quantidade de calor num período de tempo na mesma resistência.
A questão é qual seria esse valor ou como estabelecer esse valor, que depende basicamente do formato do sinal e que podemos relacionar a um equivalente DC. No sinal senoidal puro, esse valor não é o valor de pico e tampouco o valor médio (mesmo que seja a média apenas de um ciclo positivo, que não seria zero, mas 63,7% do valor de pico).
Como a própria definição do valor eficaz envolve o conceito de potência, que é diretamente proporcional ao quadrado do valor da tensão ou da corrente (P=U^2/R ou P = I^2 x R) e levando em conta que elevando-se ao quadrado qualquer valor instantâneo da tensão ou da corrente alternada (mesmo que sejam valores negativos) automaticamente resultará em número positivo e portanto estes passíveis de se obter um média diferente de zero em qualquer situação, bastaria calcular os quadrados, fazer a média e tirar a raiz quadrada para se obter um valor. Assim, com essa operação de tirar a raiz da média dos quadrados se obteria o valor eficaz do sinal alternado, que dissiparia a mesma potência média numa resistência que um sinal contínuo. Raiz da média dos quadrados, em inglês "root mean squared" cujas iniciais formam o famoso rms.
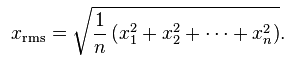
Usando essa metodologia seria possível calcular o valor eficaz de diversas formas de onda. No caso de uma onda senoidal, faria-se a integração no intervalo de 0 a 2 x pi (ou 360 graus) da função seno ao quadrado, se tiraria a média e em seguida a raiz quadrada. Desenvolvendo essa integral definida**, chega-se a uma relação entre o valor de pico da senóide e seu valor eficaz (ou rms):
Valor eficaz = Valor de pico / raiz quadrada de 2 ou
Valor eficaz = Valor de pico x 0,707
No caso de uma onda quadrada simétrica (positiva e negativa), o valor eficaz é igual ao valor de pico.
Assim, as tensões da rede elétrica são especificadas em tensão eficaz, assim como os aparelhos de medição (multímetros, voltímetros e amperímetros) nas escalas em AC também medem a tensão e corrente eficazes, eletrodomésticos, máquinas, equipamentos eletrônicos, transformadores, etc todos vem especificados em termos de valor eficaz. Uma tensão de tomada de 220Vac significa que são 220V eficazes ou 220Vrms. Note que 220Vrms tem valor de pico de 220 x 1,414 = 311V de pico e varia continuamente entre -311V a +311V em 60Hz.
Normalmente um aparelho medidor comum vai realizar uma medida apenas lendo o valor máximo ou médio e realizando uma conversão para o valor eficaz. Entretanto se a forma de onda não for perfeitamente senoidal, o valor medido apresentado estará errado, pois a calibração deles é ajustada para onda senoidal. Para contornar isso, existem aparelhos que fazem uma medição mais precisa do valor eficaz independentemente da forma de onda. Esses medidores são chamados de true rms (rms verdadeiro) e realizam diversas medições da tensão ou corrente instantânea através de amostragens e realizam o processo de cálculo descrito anteriormente para em seguida apresentar o valor eficaz. Mesmo assim, como são feitas algumas amostras, há uma limitação na frequência máxima do sinal que pode ser medido sem muito erro. Apesar de que o valor eficaz independe da frequência, o medidor ao realizar poucas amostras, pode chegar a um valor errado, devido ao aliasing.
Para ilustrar o processo de cálculo de um valor rms de uma forma de onda, exemplifico abaixo, tomando-se 12 amostras espaçadas igualmente no tempo de um sinal AC de 220Vrms (valor de pico de 311,13V):
Amostra valor valor ao
graus instantâneo (V) quadrado
000 +000,00 00000
030 +155,56 24200
060 +269,44 72600
090 +311,13 96800
120 +269,44 72600
150 +155,56 24200
180 0000,00 00000
210 -155,56 24200
240 -269,44 72600
270 -311,13 96800
300 -269,44 72600
330 -155,56 24200
12 amostras soma = 580800
média = 580800/12 = 48400
raiz 48400 = 220Vrms
O cálculo acima, apesar de conter poucos valores instantâneos, chega a um valor exato do valor eficaz, mas ideal é ter mais pontos caso o sinal seja mais complexo ou com distorção harmônica.
Alguns osciloscópios digitais também apresentam a medição do valor eficaz automaticamente, mas osciloscópios analógicos (com traço contínuo) sempre vão apresentar a forma de onda real, com valores instantâneos reais. ou seja se visualiza na tela os valores de pico (a pico).
Além das grandezas tensão e corrente alternadas, o valor eficaz pode ser empregado também em outras grandezas de natureza oscilatória, como por ex. vibração (aceleração rms) mas é muito incorretamente usada com a potência. A potência real ou média não deve ser usada com rms, apenas watt. Não existe watt rms. A multiplicação de Vrms por Arms é igual apenas a watt.
Resumo:
para onda senoidal sem nivel DC:
Veficaz = Vpico x 0,707
Veficaz = Vpico a pico / 2,828
Vmedio = Vpico x 0,637 (para só um semi ciclo simétrico)
Veficaz = Vmedio x 1,11
** Aqui a demonstração de como se chega no valor de 0,707 por integração:


